III МОДУЛЬ

Математикалық статистика

 

I-блок.   Негізгі ұғымдар. Таңдамалық әдіс

 

17-сабақ.  Бас жинақ. Таңдама жинақ  

 

 

        

Математикалық статистикада дискреттi немесе үзiлiссiз сандық сипатты белгi Х, яғни, осы белгiнiң мүмкiн мәндерiнен тұратын бас жинақ зерттелiнедi. Оның бас орташа, бас дисперсия т.с.с. сандық сипаттамаларын табу  мәселесi практикалық қажеттiлiктен туындайды.

Алайда, көп жағдайда бас жинақты толық анықтау мүмкiн емес, немесе оны анықтау көп жағдайда тиiмсiз болады. Сондықтан, осы бас  жинақтан варианталар деп аталынатын x₁,x₂,...,x_k элементтерiнен тұратын жиынша кездейсоқ терiлiп алынады. Бұл жиыншада x₁ вариантасы n₁ рет, x₂ вариантасы n₂ рет, т.т., x_к вариантасы n_к рет қайталануы мүмкiн. Онда осы жиыншаны былай жазып

 

xi	x1	x2	x3	...	xk
ni	n1	n2	n3	...	nk

 

вариациялық қатар түрiнде жазылған таңдама деймiз.

         Мұндағы n_i - x_i вариантасының жиiлiгi деп, ал n= таңдаманың көлемi деп аталады.

         Ендi осы таңдаманың сандық сипаттамалары арқылы бас жинақты  зерттеуге болады. Осы таңдамалық тәсiл - математикалық статистиканың негiзгi тәсiлi болып табылады.  

 

18-сабақ.    Таңдаманың сандық сипаттамалары. Үлестірім функциясы 

 

а) Эмпирикалық функция

       (3.1.1)

Мұнда  n_x   Х-тан кiшi болатын варианталардың жиiлiктерiнiң қосындысы. таңдаманың  көлемi үлкен болғанда, осы функция арқылы бас жинақтың белгiсiз интегралдық үлестiрiм функциясы F(x) -ты жуықтап табуға болады.

б) Жиiлiктер полигоны.

         Жазықтықтағы координаталары (x₁,n₁), (x₂,n₂),..., (x_k,n_k)  нүктелерiн қосатын кесiндiлерден тұратын қисық сызық полигон деп аталады.

в) таңдамалық орташа                                                        

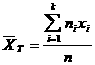     (3.1.2)

         г) таңдамалық дисперсия

     (3.1.3)

         д) таңдамалық орташа квадраттық ауытқу.

     (3.1.4)         е) к-шы реттi бастапқы эмпирикалық момент

М_к= , к=1,2,3,...     (3.1.5)

         ж) к -шы реттi орталық эмпирикалық момент

         m_к= к=1,2,3,..      (3.1.6)

         з) таңдамалық асимметрия

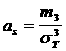<      (3.1.7)

         и) таңдамалық эксцесс

     (3.1.8)

         Ескерту 1. Егер Х_i варианталары үлкен сандар болса, жоғарыдағы (3.1.3) формулаларын тiкелей пайдаланбай,u_i = x_i - c деген шартты варианталарға көшiп, мына формулаларды пайдаланған ыңғайлы болады

     (3.1.9)

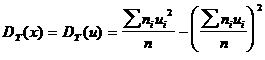     (3.1.10)

 

Мұндағы  С - "жалған нөл" деп аталынатын сан, оны өзiмiз жиiлiгi ең үлкен варианталарына шамалас етiп таңдаймыз.

         Мысал 1. таңдама мына вариациялық қатар түрiнде  берiлген:

 

xi	1	4	5
ni	4	4	2

 

Барлық сипаттамаларын табыңыз.

         Шешуi:  x_i варианталары кiшкене сандар болғандықтан (3.1.1) - (3.1.8) формулаларын тiкелей қолданамыз.

а) таңдаманың көлемi n=10 және x £ 1 болса n_x=0 (1-ден кiшi варианталар жоқ), демек          F*(x)=0 , ал x<4 болса n_x = 4, F*(x)=0,4, т.с.с. есептеулер жүргiзiп мына функцияны табамыз.   

                   

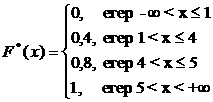
Осы функцияның графигi төмендегiдей болғандықтан, эмпирикалық функцияны баспалдақ тәрiздес функция деп атау орынды.

 

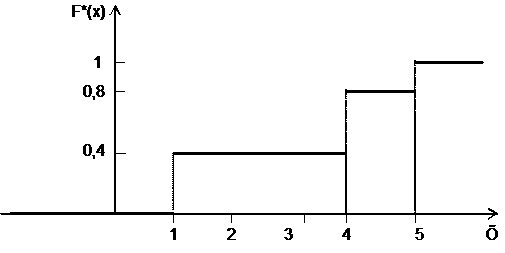
б) Жиiлiктер полигоны төмендегiдей қисық болады.

 

 

в)

г)

д)

е)

ж) ,      

  

  

з)

и)

Мысал 2. Берiлген вариациялық қатар арқылы х_Т мен D_T  -ны табыңыз.

 

xi	3860	3900	3910	3913
ni	2	13	4	1

 

Шешуi: Варианталар үлкен сандар, сондықтан С=3900 деп алып,    Ui=Xi-C шартты варианталарға көшейiк, яғни шартты вариациялық қатар аламыз.

 

Ui	-40	0	10	13
ni	2	13	4	1

 

Сонда  (3.1.9), (3.1.10) формулаларын пайдалансақ

        

         Ескерту 2. Егер сандық сипатты белгi Х үзiлiссiз таралған болса, оның бақыланған мәндерi кiретiн  интервалды үзындықтары h болатындай бiрнеше кiшi интервалдарға бөлiп, әрбiр бөлiкте жататын варианталардың жиiлiктерiнiң қосындысы n_i анықталады. Сонда  табаны (x_i;x_i+1) кiшi интервал, ал биiктiгi   болатын тiктөртбұрыштардан құралған фигураны - гистограмма деймiз.

        

Мысал 3. Мына таңдаманың гистограммасын құрыңыз.

 

Интервал нөмiрi	Кiшi интервалдар	Варианталардың жиiлiктерiнiң қосындысы	Жиiлiктер тығыздығы
i	(xi ; xi+1)	ni	ni /h
1 2 3	(1 ; 5) (5; 9) (9; 13)	20 30 50	5 7,5 12,5

 

Шешуi: Абциссалар осiнде ұзындықтары 4 болатын берiлген интервалдарды саламыз. Ендi табандары осы интервалдар болатын ал  биiктiктерi   болатын тiктөртбұрыштарды саламыз.

 

<-

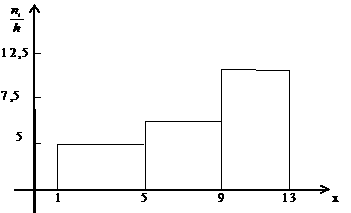
 Гисторамманың ауданы  n кв.өлшем бiрлiгiне тең болады.

 

II-блок.   Үлестірім параметрлерін бағалау

 

19-сабақ.   Нүктелік бағалау 

 

         Дискреттi немесе үзiлiссiз сандық сипатты белгi Х-ың үлестiрiмiнiң белгiсiз параметрiн Ɵ деп белгiлейiк. Оның таңдама арқылы табылатын нүктелiк  бағасы Ɵ* болсын. Әртүрлi таңдамалар үшiн өзгерiп отыратындықтан Ɵ* - кездейсоқ шама болады.

         Анықтама 1. Егер М(Ɵ*)= Ɵ болса, онда Ɵ* жылжымаған баға деп аталады, ал басқа жағдайда жылжыған баға деп аталады.

         Анықтама 2. Егер  болса, онда Ɵ* орнықты баға деп аталады, бұл жерде n - таңдама көлемi.

 

         Сөйлем 1. Бас орташаның жылжымаған және орнықты нүктелiк бағасы таңдамалық орташа болады.

         Сөйлем 2. Бас дисперсияның жылжыған бағасы таңдамалық дисперсия болады, ал жылжымаған бағасы түзетiлген таңдамалық дисперсия s² болады, мұнда  n - таңдама көлемi.

         Мысал 1.  Бас жинақтан мынадай таңдама алынған.

 

xi	4	5	7
ni	10	5	5

 

         а) Бас  орташаның  жылжымаған бағасын табыңыз.

         б) Бас дисперсияcының жылжымаған  және  жылжыған бағаларын табыңыз.

         Шешуi:

а) таңдамалық орташа жылжымаған баға болады.

                  

б) Жылжыған баға ретiнде D_T, ал жылжымаған баға ретiнде s² алынады

                   ,    

 

         Моментер әдісі

 

         Бұл әдiс бастапқы және орталық эмпирикалық моменттер өздерiне сәйкес бастапқы және орталық теориялық моменттердiң орнықты бағалары болатындығына негiзделген. Осы  сәйкес  моменттердi бiр-бiрiне теңестiре отырып, үлестiрiмнiң белгiсiз параметрiнiң нүктелiк бағалауларын табуға болады.

         Мысал 1. Көрсеткiштiк үлестiрiмнiң белгiсiз параметрi   l- ның нүктелiк бағасын табыңыз.

         Шешуi: Бастапқы I-шi реттi эмпирикалық және теориялық моменттердi теңестiремiз.

                                      n₁=M₁

Көрсеткiштiк  үлестiрiмнiң бiрiншi  реттi бастапқы моментi

n₁=M(x)= , ал M₁=   болғандықтан =   теңдiгiн аламыз. Осыдан белгiсiз параметр  l-ның нүктелiк бағасы l*=   тең.

Мысал 2. Берiлген таңдама бойынша моменттер әдiсiн қолданып  қалыпты үлестiрiмнiң

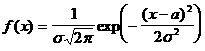
белгiсiз a және s параметрлерiнiң  нүктелiк бағасын табыңыз.

Шешуi: Бұл жағдайда екi а  және s белгiсiз параметр болғандықтан бiрiншi, екiншi реттi теориялық және эмпирикалық  моменттердi теңестiремiз.

n₁=M₁, m₂=m₂.

Ары қарай  n₁=M(x)=a, m₂=D(x)= s²  және M₁= , m₂=D_T екенiн eскерсек, онда  мынадай нүктелiк бағалар аламыз

a*= , s*=

Мысал 3. Берiлген  таңдамасының сипаттамалары арқылы моменттер әдiсiмен бiрқалыпты үлестiрiмнiң

                           

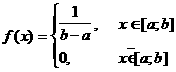
белгiсiз a және b параметрлерiнiң нүктелiк бағаларын табыңыз.

Шешуi: Бiрiншi және екiншi реттi эмпирикалық моменттердi теориялық моменттерге  теңестiрейiк, яғни n₁=M₁, m₂=m₂.  

Сонда n₁=M(x)= , m₂=D(x)= , M₁= , m₂=D_T екенiн  ескере отырып мынадай  теңдеулер системасын аламыз: 

Осы системаны шеше отырып, a*= - ,   b*= + нүктелiк бағаларын табамыз.

20-сабақ.   Интервалдық бағалау 

 

         Бiр санмен ғана  анықталатын  нүктелiк  баға, таңдаманың  көлемi аз болғанда,  өрескел қатеге соқтыруы мүмкiн, сондықтан бас жинақтың белгiсiз параметрiнiң  интервалдық  бағасын,  яғни  осы  q  параметрi  жататындай (a,b) интервалын белгiлi бiр сенiмдiлiкпен айқындау мәселесiн қарастырайық.

Анықтама 1. q параметрiнiң q* бағасы бойынша сенiмдiлiгi (сенiмдiлiк ықтималдығы) деп ½q-q*½<d теңсiздiгiнiң орындалу ықтималдығы g- ны  айтады, яғни Р(½q-q*½< d)=g, бұл жерде d - бағаның дәлдiгi.

Анықтама 2. (q*-d, q*+d) - интервалын g сенiмдiлiгiмен алынған сенiмдiлiк интервалы деп атайды.

Сөйлем 1. Қалыпты үлестiрiммен берiлген сандық сипатты белгi Х шаманың  белгiсiз а  математикалық үмiтiн таңдамалық орташа  арқылы   g сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз.

а) Егер  s - бас орташа квадраттық ауытқу белгiлi болса, онда

     (4.4.1)

t-саны Ф(t) =  -ға тең болатындай  сан, оны Лаплас функциясының   мәндер кестесiнен аламыз.

 

б) Егер s - белгiсiз болса, онда

     (4.4.2)

Мұнда S - түзетiлген таңдамалық орташа квадраттық ауытқу,  - шамасы кестеден анықталады.

Сөйлем 2. Қалыпты үлестiрiммен берiлген Х-тың бас орташа квадраттық ауытқуы s -ны берiлген g сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз.

 

s(1-q)< s<s(1+q) , егер  q<1      (4.4.3)

0<s<s(1+q) ,  егер q>1      (4.4.4)

 

Бұл жерде  q=q(n,g) - кестеден  алынады.

Мысал 1. Бас орташа квадраттық ауытқуы s = 5 болатын қалыпты үлестiрiммен берiлген бас жинақтан алынған  көлемi n=25  таңдамадан  =17 табылды. Бас жинақтың белгiсiз математикалық  үмiтiн g=0,99 сенiмдiлiгiмен бағалайтын  интервалын табыңыз.

Шешуi: (4.4.1) формуласын пайдаланамыз. Егер ,  онда кестеден t=2,57, яғни

Ocыдан   сенiмдiлiк интервалы.

Мысал 2. Әлдебiр физикалық шама бiр құралмен 10 рет өлшенедi. Өлшеулердiң кездейсоқ қателерiнiң түзетiлген орташа квадраттық ауытқуы  0,5 - ке тең. Өлшеу құралының дәлдiгiн g=0,99 сенiмдiлiгiмен табыңыз.

Шешуi: Құралдың дәлдiгi  өлшеуде жiберiлген кездейсоқ қателердiң бас орташа квадраттық ауытқуымен сипатталады, яғни бiзге s -ны бағалайтын сенiмдiлiк интервалын табу керек.

g=0,99, n=10 болса, кестеден q=1,08 олай болса, (4.4.4) формуласын пайдалана отырып 0<s<1,04 дәлдiктi анықтайтын сенiмдiлiк интервалын табамыз.

 

p style='text-align:justify;mso-pagination:none;mso-layout-grid-align: none;text-autospace:none'> 

III-блок.   Статистикалық болжамдар

 

21-сабақ.   Пирсон Хи-квадрат критерийі 

 

 

 

         Анықтама 1. Статистикалық  болжам деп кездейсоқ шаманың үлестiрiмiнiң түрi немесе үлестiрiм параметрлерi туралы алдын-ала жасалатын болжамды айтады. Статистикалық болжам таңдаманың көмегiмен тексерiледi.

         Алдымен нөлдiк болжам деп аталатын, тексерiлуге  тиiс Но болжамы қарастырылады. Бұл болжамға қарсы болжамды альтернативтi  деп атап, Н₁  әрiпiмен белгiлеймiз. Мысалы: үлестiрiмнiң белгiсiз параметрi q туралы нөлдiк болжам былай болса Но: q= qо , онда Н₁ : q ¹ qо (Н₁: q>< qo).

         Cтатистикалық  болжамды тексеру барысында екi түрлi қате жiберуiмiз мүмкiн.

         Бiрiншi тектi қате -  Но болжамы жоққа шығарылып Н₁ болжамы қабылданады,  бiрақ негiзiнде Но дұрыс.

         Екiншi тектi қате - Но болжамын қабылдаймыз, бiрақ негiзiнде Н₁   болжамы дұрыс.

         Анықтама 2. Бiрiншi тектi қате  жiберу ықтималдығын маңыздылық  деңгейi  деймiз де, a әрiпiмен белгiлеймiз.

         Болжамды тексерудiң жалпы схемасы:

1     Үлестiрiмi белгiлi статистикалық критерий деп аталатын F кездейсоқ шамасы енгiзiледi. Бұл шаманың әртүрлi еркiндiк дәрежелерi болып, ал үлестiрiмi қалыпты, хи - квадрат, Стьюдент, Фишер-Снедекорүлестiрiмдерiмен  берiлуi   мүмкiн.

2     таңдамалық (эмпирикалық) белгiлi деректерге сүйене отырып, критерийдiң  бақыланатын  мәнi  F_бақ анықталады.

3     Берiлген a  маңыздылық  деңгейiнде  F  үлестiрiмiнiң сын нүктелерi кестесi арқылы, критерийдiң сындық мәнi - F_сын анықталады.

4     Егер F_бақ<F_сын болса,  онда Но  болжамын жоққа шығару негiз жоқ, ал егер F_бақ>F_сын болса, онда Но болжамы қабылданбайды.

                Егер  үлестiрiм заңы белгiсiз болса, онда "бас жинақ А заңы бойынша үлестiрiлген", - деген нөлдiк болжам келiсiмдiк  критерийлерi арқылы тексерiледi. Олардың бiрнеше түрi бар: Пирсон критерийi, Колмогоров критерийi, Смирнов критерийi т.т.

         Но: "бас жинақ қалыпты үлестiрiммен берiлген" деген болжамды тексеру  үшiн Пирсонның  келiсiмдiк  критерийi қолданылады.

         Сонымен h  қадамымен бiркелкi орналасқан таңдама берiлсiн

 

хi	х1	х2	х3	...	хm
ni	n1	n2	n3	...	nm

 

Ендi  теориялық жиiлiктердi табамыз.

немесе

Осыдан мына кесте анықталады:

 

Эмпирикалық жиiлiктер	N1	n2	n3	...	nm
Теориялық жиiлiктер				...

 

                Теориялық  және эмпирикалық  жиiлiктердiң бiр-бiрiнен ауытқуы кездейсоқ па, бақылаулар саны аз ба, әлде  "бас жинақ қалыпты  үлестiрiммен берiлген" деген нөлдiк болжам дұрыс емес пе? Осы сұрақтарға Пирсон критерийi жауап бередi.

 

Тексеру схемасы:

 

2.Статистикалық критерий  ретiнде мына кездейсоқ шаманы аламыз

     (5.2.1)

Бұл шама - еркiндiк дәрежесi к=s-1-r болатын, хи - квадрат үлестiрiмiмен таралған кездейсоқ шама. Мұнда s - таңдамадағы топтар саны, r - үлестiрiм параметрлерiнiң саны.

2.Берiлген деректерге сүйене отырып, критерийдiң бақыланатын мәнiн анықтаймыз.

     (5.2.2)>

3. Берiлген a  маңыздылық деңгейiнде, хи - квадрат үлестiрiмнiң  сын нүктелерi кестесi арқылы  критерийдiң сындық мәнiн анықтаймыз.

4. Егер  <  - нөлдiк  болжамды жоққа шығаруға  негiз жоқ, ал егер > - нөлдiк болжам қабылданбайды.

Мысал. 1. Эмпирикалық және теориялық  жиiлiктер берiлген

 

Эмпирикалық жиiлiктер	5	13	39	75	105	83	32	14
Теориялық жиiлiктер	3	15	41	80	101	77	38	13

 

Берiлген a=0,05 маңыздылық  деңгейiнде бас жинақтың қалыпты үлестiрiлгендiгi  туралы болжамды тексерiңiз.

Шешуi:  Критерийдiң бақыланатын мәнiн анықтау үшiн төмендегi кестенi құрамыз.

 

1 2 3 4 5 6 7 8	5 13 39 75 105 83 32 14	3 15 41 80 101 77 38 13	2 -2 -2 -2 4 6 -6 1	4 4 4 25 16 36 36 1	1,333 0,267 0,097 0,3125 0,158 0,468 0,947 0,077

        

Сонымен =3,66, ал критерийдiң  еркiндiк дәрежесi к=s-1-r=5, себебi s = 8, r = 2 (қалыпты үлестiрiм екi параметр  арқылы анықталады). Онда кестеден  (0,05; 5)=11,1. Сонымен < - нөлдiк  гипотезаны жоққа шығаруға негiз жоқ. Алдыңғы 1-мысалда теориялық және эмпирикалық жиiлiктер берiлген. Ендi тек эмпирикалық жиiлiктер белгiлi болғанда теориялық жиiлiктердi қалай есептеуге болатындығын көрсетелiк.

Мысал 2. Интервалдық вариациялық қатар (III-тарау,1-кесте) мына түрде берiлген:        

 

	0-5	5-10	10-15	15-20	20-25
	10	21	35	22	12

 

Пирсон критерийiн қолданып маңыздылық деңгейi  болғанда сандық белгiнiң бақыланған мәндерiн пайдаланып “бас жинақ қалыпты үлестiрiммен берiлген” -деген нөлдiк болжамды тексерiңiз.

         Шешуi.

1.   Бас жинақтың үлестiрiм заңы туралы болжам жасау үшiн, бiрiншiден, полигон және гистограмманың түрiне қараймыз. Мысалы, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасау үшiн:

  а) гистограмманың түрi Гаусс қисығының түрiне ұқсас болуы керек

  б) эмпирикалық ассиметрия мен экцесс мына теңсiздiктердi

        және   қанағаттандыруы керек.

Мұндағы

,

Қарастырып отырған мысал үшiн

, - , ал ,

олай болса және  .

        Ендi гистограммаға қарасақ  (III тарау, §1), оның түрi Гаусс қисығына ұқсас. Демек, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасауға негiз бар.

 

2.   Ендi нөлдiк болжамды тексеру үшiн Пирсон критерийiн қолданамыз. Ол үшiн

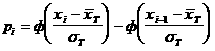,  формулаларын қолданып теориялық жиiлiктердi есептеймiз.

Белгiлеу енгiзелiк ,

Есептеу кестесiн құрамыз.

Интер-валдар
0-5	10	-2,23	-1,35	-0,4870	-0,4115	0,0755	8
5-10	21	-1,35	-0,48	-0,4115	-0,1844	0,2277	23
10-15	35	-0,48	0,39	-0,1844	0,1517	0,3361	34
15-20	22	0,39	1,27	0,1517	0,3980	0,2463	25
20-25		1,27	2,14	0,3980	0,4838	0,0858

_бақ есептеу үшiнде есептеу кестесiн жазған тиiмдi

 

1	10	8	2	4	0,5
2	21	23	-2	4	0,17
3	35	34	1	1	0,03
4	22	25	-3	9	0,36
5	12	9	3	9	1
					1,7

Сонда _бақ=1,7.

          Ендi  маңыздылық  деңгейiнде  еркiндiк дәрежесi бойынша _сын(0,05;2) кiтап соңындағы кестеден анықтаймыз:

_сын(0,05;2)=6. Осыдан _бақ< _сын екенiн көремiз. Демек, бас жинақтың қалыпты үлестiрiммен берiлгендiгi туралы нөлдiк болжамды қабылдамауға негiз жоқ.

Жаттығу есептері

 

1. Мына  таңдаманың сипаттамаларын және эмпирикалық функциясын  табыңыз.

xi	-1	1	2	3
ni	3	4	2	1

 

2. Қалыпты үлестiрiлген бас жинақтың орташа квадраттық ауытқуын s, таңдамалық орташасын , түзетiлген таңдамалық орташа квадраттық ауытқуын  s, таңдама көлемiн  n  деп алып, белгiсiз математикалық үмiт а - ны бағалайтын сенiмдiлiк интервалдарын табыңыз.

а) s= 4,     10,2 ,   n=16,    g=0,99

б) s = 5,    16,8 ,   n=25,    g=0,95

в) s = 3,    12 ,     n=9,      g=0,99

г) s = 7,2,   10 ,     n=40,    g=0,95

 

 

...